DoPrep

Question Asked by a Student:-

A 2 by 2 determinant is chosen such that the elements are from the set {-1, 1}. Find the probability of choosing determinants whose value is 0?

Solution:-

Based on DoPrep’s method of problem solving strongly influenced by the works of the great Hungarian Mathematician George Pólya.

The following conversation between the student and DoPrep illustrates our Art of Problem Solving and how it helps the student to understand and retain the applied concept.

Step 1 :- Understand the Problem

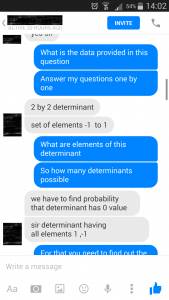    The student answered the questions

1) What is the input given in this question?

We have been given a 2 by 2 determinant whose elements             are from the set {1, -1}

2) What is the output required from the questions?

We have been asked to find out the probability that                         determinant has 0 value

 

 

Step 2:- Make the Plan 

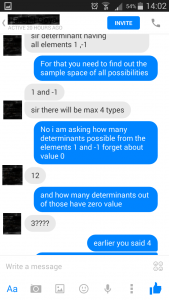    The conversation between the student and DoPrep was                 centered around finding the link between the input and the           output

1) The concept link between the input and out was to find out            the total number of possible determinants (total sample                space) and the number of cases for which the determinant’s          value is zero

2) Then in order to find out the probability we needed to                    divide the two cases mentioned in point 1).

 

 

Step 3:- Carry out the Plan 

 

 

 

 

 

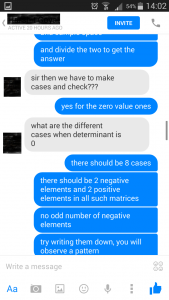
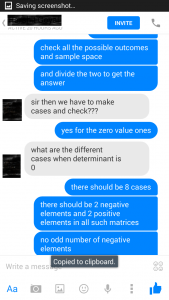
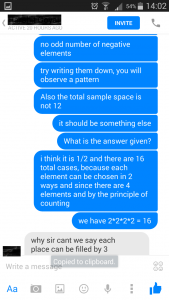
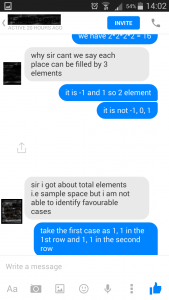
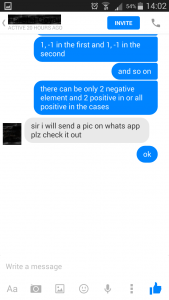
In this step, the conversation in between the student and DoPrep was centered on finding out

1) The total number of 2 by 2 determinants that be made from the elements 1, -1

This came out to be 2^4 = 16 as each of the element in the determinant can be chosen     in 2 ways

2) The total number of 2 by 2 determinants that be made from the elements 1, -1 and            whose value is 0

This came out to be 8 after listing down all such cases which have either all positive           elements (i.e. 1), or having all negative elements (i.e. -1) or having even number of             negative elements ( i.e. 2 elements are -1 and the remaining 2 are 1)

3) Then by definition of probability the student found out the answer by dividing 8 by 16      to get 1/2

Step 4 :- Look back at it? How could it be better
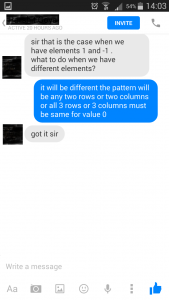After the output was achieved the student by himself extended this question to a 3 by 3 determinant and asked DoPrep if the procedure would be the same for this case also.

We then found out that

1) any two rows or two columns or all 3 rows or 3 columns must be the same in order to find out the number of determinants whose value is 0.

(A little help from another concept, properties of determinants, was taken in order to solve this question based on probability)

 

 

 

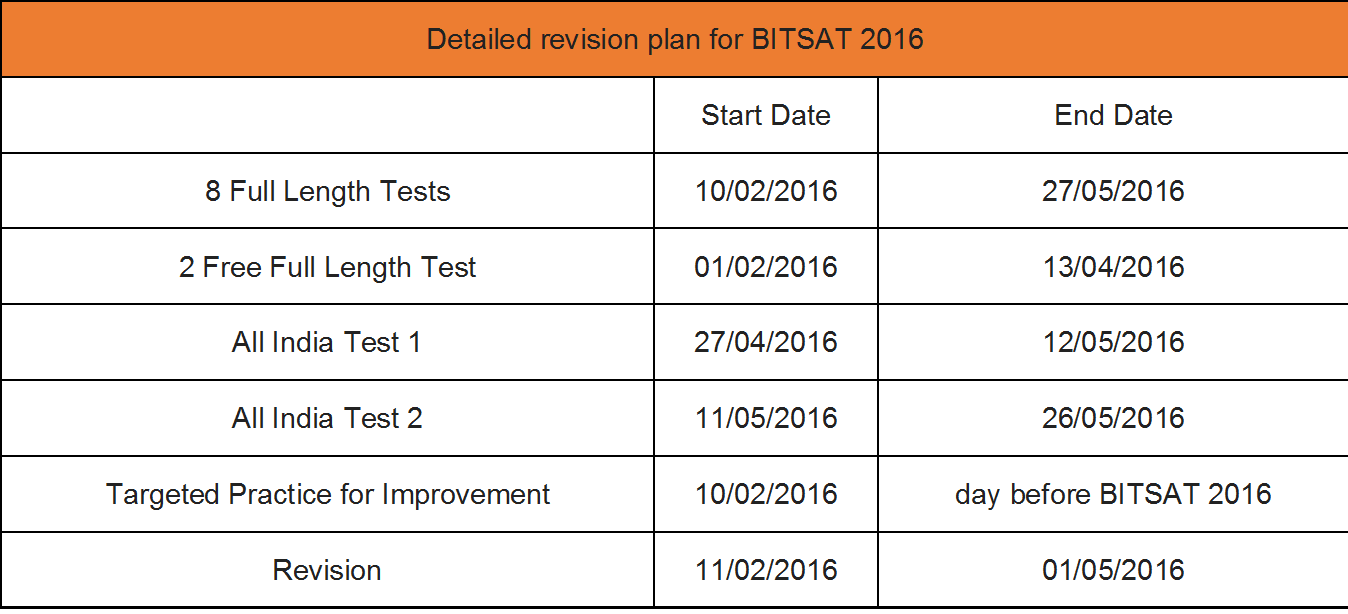
So what are you waiting for? Get ahead with DoPrep JEE (main) and BITSAT 2016 test series.

Buy Now!

OR

Take a free JEE test now to experience it! 

OR

Take a free BITSAT test now to experience it! 

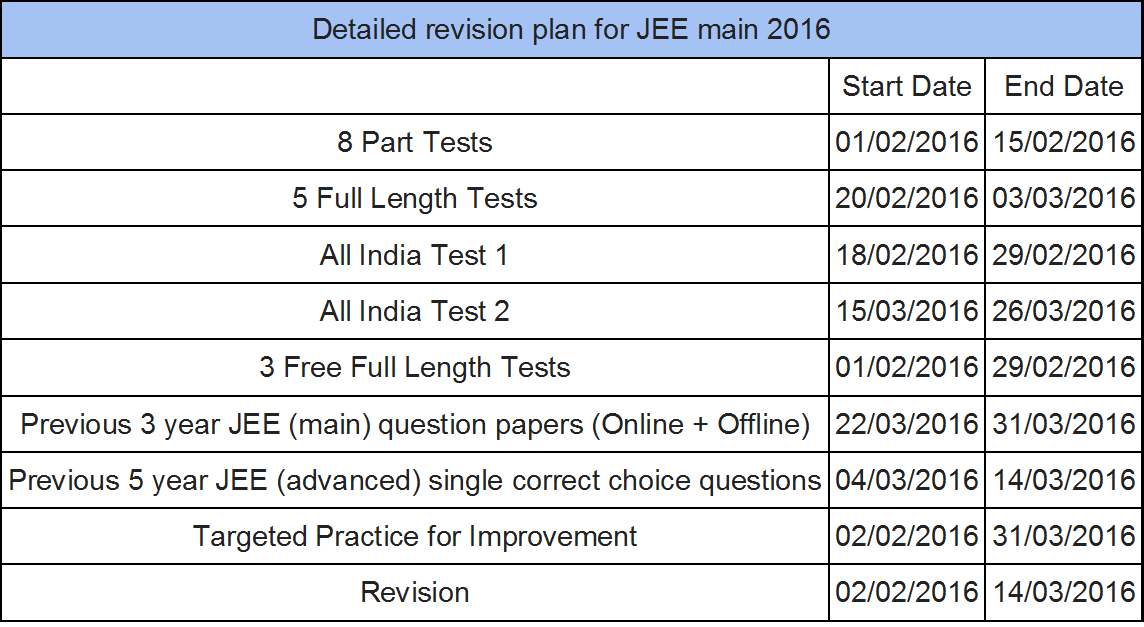
JEE main 2016 detailed improvement plan

Best wishes,

DoPrep